MATEMÁTICA II
Um capital de R$ 80 000, 00 foi aplicado a juros compostos e à taxa anual de 15%, após quanto tempo aproximadamente, em anos, da aplicação serão obtidos juros no valor de R$ 70 000, 00?
Dica: Montante = capital + juros e M = C(1+i)n .
5,5
5
4,5
3,5
4
Seja  então os valores que x pode assumir são:
então os valores que x pode assumir são:
3 e 5
-2 e 5
-5 e 2
1 e 2
2 e 5
Considere a inequação  . O conjunto solução da inequação dada é:
. O conjunto solução da inequação dada é:





O conjunto solução S da inequação  é dada por:
é dada por:





Seja  a função definida por
a função definida por%7D%7D%7D%3D%5Cfrac%7B%7B%7Bx%7D-%7B1%7D%7D%7D%7B%7B%7Bx%7D%2B%7B2%7D%7D%7D) . O valor de f -1 (2) é exatamente:
. O valor de f -1 (2) é exatamente:
-5
3
6
-1
-7
Seja a função f: R R definida pela lei de formação: %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B3%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B0%7D%5C%5C%7B4%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7Bx%7D%2B%7B5%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B0%7D%7D%5Cright.%7D)
Se N = f(-2 ) + f(1) - f(0) - f(3) então N é igual a:
24
14
20
16
21
Seja f(x) uma função definida por várias sentenças cujo o esboço segue abaixo:
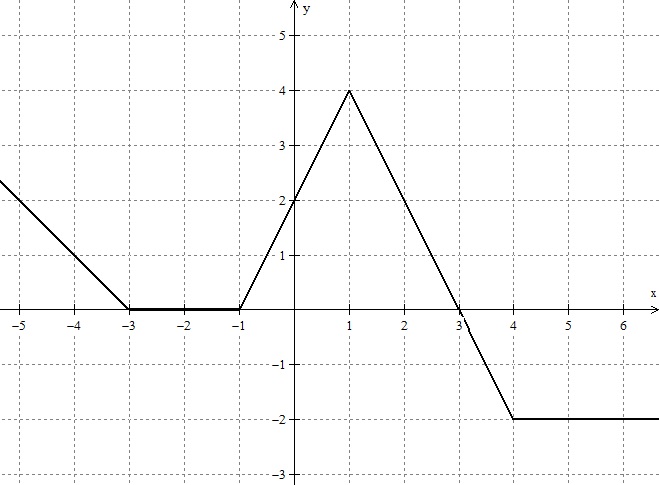
Se E = f(- 4) + f(-2) + f(0) + f(1) - f(2) + f(4) + f(5) então o valor de E é exatamente:
- 2
3
-1
5
1
Uma equação modular é toda equação cuja incógnita se apresenta em módulo, considere a equação 
O conjunto solução que satisfaz a equação é dado por:
S = {-3, -2, 1, 2}
S = {-2, 1, 2}
S = { } (vazio)
S = {-1, 1, 2}
S = {-3, -1, 2, 3}
Suponha que a equação  , seja válida para todo número real x, em que a,b e c são números reais. Então, a soma
, seja válida para todo número real x, em que a,b e c são números reais. Então, a soma  é igual a
é igual a
5,5
5
4,5
3,5
4
Seja  então os valores que x pode assumir são:
então os valores que x pode assumir são:
3 e 5
-2 e 5
-5 e 2
1 e 2
2 e 5
Considere a inequação  . O conjunto solução da inequação dada é:
. O conjunto solução da inequação dada é:





O conjunto solução S da inequação  é dada por:
é dada por:





Seja  a função definida por
a função definida por%7D%7D%7D%3D%5Cfrac%7B%7B%7Bx%7D-%7B1%7D%7D%7D%7B%7B%7Bx%7D%2B%7B2%7D%7D%7D) . O valor de f -1 (2) é exatamente:
. O valor de f -1 (2) é exatamente:
-5
3
6
-1
-7
Seja a função f: R R definida pela lei de formação: %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B3%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B0%7D%5C%5C%7B4%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7Bx%7D%2B%7B5%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B0%7D%7D%5Cright.%7D)
Se N = f(-2 ) + f(1) - f(0) - f(3) então N é igual a:
24
14
20
16
21
Seja f(x) uma função definida por várias sentenças cujo o esboço segue abaixo:

Se E = f(- 4) + f(-2) + f(0) + f(1) - f(2) + f(4) + f(5) então o valor de E é exatamente:
- 2
3
-1
5
1
Uma equação modular é toda equação cuja incógnita se apresenta em módulo, considere a equação 
O conjunto solução que satisfaz a equação é dado por:
S = {-3, -2, 1, 2}
S = {-2, 1, 2}
S = { } (vazio)
S = {-1, 1, 2}
S = {-3, -1, 2, 3}
Suponha que a equação  , seja válida para todo número real x, em que a,b e c são números reais. Então, a soma
, seja válida para todo número real x, em que a,b e c são números reais. Então, a soma  é igual a
é igual a
3 e 5
-2 e 5
-5 e 2
1 e 2
2 e 5
Considere a inequação  . O conjunto solução da inequação dada é:
. O conjunto solução da inequação dada é:





O conjunto solução S da inequação  é dada por:
é dada por:





Seja  a função definida por
a função definida por%7D%7D%7D%3D%5Cfrac%7B%7B%7Bx%7D-%7B1%7D%7D%7D%7B%7B%7Bx%7D%2B%7B2%7D%7D%7D) . O valor de f -1 (2) é exatamente:
. O valor de f -1 (2) é exatamente:
-5
3
6
-1
-7
Seja a função f: R R definida pela lei de formação: %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B3%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B0%7D%5C%5C%7B4%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7Bx%7D%2B%7B5%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B0%7D%7D%5Cright.%7D)
Se N = f(-2 ) + f(1) - f(0) - f(3) então N é igual a:
24
14
20
16
21
Seja f(x) uma função definida por várias sentenças cujo o esboço segue abaixo:

Se E = f(- 4) + f(-2) + f(0) + f(1) - f(2) + f(4) + f(5) então o valor de E é exatamente:
- 2
3
-1
5
1
Uma equação modular é toda equação cuja incógnita se apresenta em módulo, considere a equação 
O conjunto solução que satisfaz a equação é dado por:
S = {-3, -2, 1, 2}
S = {-2, 1, 2}
S = { } (vazio)
S = {-1, 1, 2}
S = {-3, -1, 2, 3}
Suponha que a equação  , seja válida para todo número real x, em que a,b e c são números reais. Então, a soma
, seja válida para todo número real x, em que a,b e c são números reais. Então, a soma  é igual a
é igual a
O conjunto solução S da inequação  é dada por:
é dada por:





Seja  a função definida por
a função definida por%7D%7D%7D%3D%5Cfrac%7B%7B%7Bx%7D-%7B1%7D%7D%7D%7B%7B%7Bx%7D%2B%7B2%7D%7D%7D) . O valor de f -1 (2) é exatamente:
. O valor de f -1 (2) é exatamente:
-5
3
6
-1
-7
Seja a função f: R R definida pela lei de formação: %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B3%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B0%7D%5C%5C%7B4%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7Bx%7D%2B%7B5%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B0%7D%7D%5Cright.%7D)
Se N = f(-2 ) + f(1) - f(0) - f(3) então N é igual a:
24
14
20
16
21
Seja f(x) uma função definida por várias sentenças cujo o esboço segue abaixo:

Se E = f(- 4) + f(-2) + f(0) + f(1) - f(2) + f(4) + f(5) então o valor de E é exatamente:
- 2
3
-1
5
1
Uma equação modular é toda equação cuja incógnita se apresenta em módulo, considere a equação 
O conjunto solução que satisfaz a equação é dado por:
S = {-3, -2, 1, 2}
S = {-2, 1, 2}
S = { } (vazio)
S = {-1, 1, 2}
S = {-3, -1, 2, 3}
Suponha que a equação  , seja válida para todo número real x, em que a,b e c são números reais. Então, a soma
, seja válida para todo número real x, em que a,b e c são números reais. Então, a soma  é igual a
é igual a
Seja  a função definida por
a função definida por%7D%7D%7D%3D%5Cfrac%7B%7B%7Bx%7D-%7B1%7D%7D%7D%7B%7B%7Bx%7D%2B%7B2%7D%7D%7D) . O valor de f -1 (2) é exatamente:
. O valor de f -1 (2) é exatamente:
-5
3
6
-1
-7
Seja a função f: R R definida pela lei de formação: %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B3%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B0%7D%5C%5C%7B4%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7Bx%7D%2B%7B5%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B0%7D%7D%5Cright.%7D)
Se N = f(-2 ) + f(1) - f(0) - f(3) então N é igual a:
24
14
20
16
21
Seja f(x) uma função definida por várias sentenças cujo o esboço segue abaixo:

Se E = f(- 4) + f(-2) + f(0) + f(1) - f(2) + f(4) + f(5) então o valor de E é exatamente:
- 2
3
-1
5
1
Uma equação modular é toda equação cuja incógnita se apresenta em módulo, considere a equação 
O conjunto solução que satisfaz a equação é dado por:
S = {-3, -2, 1, 2}
S = {-2, 1, 2}
S = { } (vazio)
S = {-1, 1, 2}
S = {-3, -1, 2, 3}
Suponha que a equação  , seja válida para todo número real x, em que a,b e c são números reais. Então, a soma
, seja válida para todo número real x, em que a,b e c são números reais. Então, a soma  é igual a
é igual a
-5
3
6
-1
-7
Seja a função f: R R definida pela lei de formação: %7D%7D%7D%3D%7B%5Cleft%5Clbrace%5Cmatrix%7B-%7B2%7D%7Bx%7D%2B%7B3%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%5Cge%7B0%7D%5C%5C%7B4%7D%7B%7Bx%7D%7D%5E%7B%7B2%7D%7D-%7Bx%7D%2B%7B5%7D%26%7Bs%7D%7Be%7D%26%7Bx%7D%3C%7B0%7D%7D%5Cright.%7D)
Se N = f(-2 ) + f(1) - f(0) - f(3) então N é igual a:
24
14
20
16
21
Seja f(x) uma função definida por várias sentenças cujo o esboço segue abaixo:

Se E = f(- 4) + f(-2) + f(0) + f(1) - f(2) + f(4) + f(5) então o valor de E é exatamente:
- 2
3
-1
5
1
Uma equação modular é toda equação cuja incógnita se apresenta em módulo, considere a equação 
O conjunto solução que satisfaz a equação é dado por:
S = {-3, -2, 1, 2}
S = {-2, 1, 2}
S = { } (vazio)
S = {-1, 1, 2}
S = {-3, -1, 2, 3}
Suponha que a equação  , seja válida para todo número real x, em que a,b e c são números reais. Então, a soma
, seja válida para todo número real x, em que a,b e c são números reais. Então, a soma  é igual a
é igual a
24
14
20
16
21
Seja f(x) uma função definida por várias sentenças cujo o esboço segue abaixo:

Se E = f(- 4) + f(-2) + f(0) + f(1) - f(2) + f(4) + f(5) então o valor de E é exatamente:
- 2
3
-1
5
1
Uma equação modular é toda equação cuja incógnita se apresenta em módulo, considere a equação 
O conjunto solução que satisfaz a equação é dado por:
S = {-3, -2, 1, 2}
S = {-2, 1, 2}
S = { } (vazio)
S = {-1, 1, 2}
S = {-3, -1, 2, 3}
Suponha que a equação  , seja válida para todo número real x, em que a,b e c são números reais. Então, a soma
, seja válida para todo número real x, em que a,b e c são números reais. Então, a soma  é igual a
é igual a

- 2
3
-1
5
1
Uma equação modular é toda equação cuja incógnita se apresenta em módulo, considere a equação 
O conjunto solução que satisfaz a equação é dado por:
S = {-3, -2, 1, 2}
S = {-2, 1, 2}
S = { } (vazio)
S = {-1, 1, 2}
S = {-3, -1, 2, 3}
Suponha que a equação  , seja válida para todo número real x, em que a,b e c são números reais. Então, a soma
, seja válida para todo número real x, em que a,b e c são números reais. Então, a soma  é igual a
é igual a
S = {-3, -2, 1, 2}
S = {-2, 1, 2}
S = { } (vazio)
S = {-1, 1, 2}
S = {-3, -1, 2, 3}